RDF Store, Part 1: Implementing B-Trees

Data structures are awesome! Seriously, I know that is probably one of the most geekiest things I have ever said, it's really true. Think about it, how you store your data has a profound effect on how quickly you can retrieve it. And I'm not talking about a few seconds here and a few seconds there. I'm talking about the difference between whether an application is usable and whether an application isn't.

One of the structures which is used extensively in data stores is B-Trees. While the avant-garde is to store all data in  memory and use a transaction log to rebuild those structures when a server is restarted, B-Trees are used extensively within disk based stores.

I've been reading around efficient ways of storing data for RDF stores, and while reading a paper called RDF-3X: a RISC-style Engine for RDF, it expressed some interesting ideas of using multiple B-Trees to store  and retrieve RDF statements. I thought this would be a great basis to start making a RDF store. As we're going to be mostly cooking this from the ground up, we first need a B-Tree implementation to start off with.

I've started creating this in C# which probably isn't the best choice of language for this, we will probably move from C# to another language when we start looking at making the store multi-node etc. But for now it's a good enough prototyping language for us to play with.

What are B-Trees and why are they important?

Before we answer that, let's have a look at binary search trees (BST). While BSTs are remarkably useful, their structure is dependent on the order in which the values are inserted into the tree, rather than the values of the objects being inserted. If the values are random, this isn't a problem, as the tree roughly becomes balanced. However if the values are ordered, we end up with a vine rather than a tree, this makes look up costs disastrous.

Fig 1. BST where insertion was {3,4,2,1,5}

Fig 2. BST where the insertion was {1,2,3,4,5}

For example, if we compare Fig 1 and Fig 2. Within Fig 1. inserting {6} takes 3 compares but within Fig 2. inserting {6} takes 5 compares. These are both BSTs with the same values within them, however Fig1. is much more efficient when it comes to the compares needed to look up a value or insert a value compared to Fig 2. 

The solution to this is to have the trees become self-balancing. There are many different tree structures which are designed to be self balancing. The one which we will be looking at for this post is B-Trees.

Structure of B-Tree

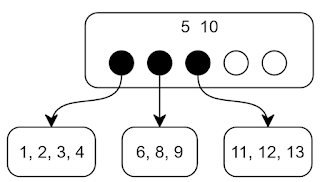Fig 3. B-Tree with d = 2

B-Trees are a self-balanced tree structure where each node contains  a variable number of keys and a number of references to other nodes. First we define the minimum  number of keys a node can hold, normally denoted by d.

Each non-leaf node contains a number of keys from d to 2d, so if we have a d = 2, the minimum size for a node is 2 and the maximum is 4. 

As well as key values, each non-leaf node keeps d  to 2d + 1 pointers to other nodes.
Fig 3, shows a simple B-Tree.

Now we have roughly defined a B-Tree, in theory, let's start spec-ing out some simple code for a B-Tree. We'll do this in C# for the moment.

So we define a simple node class and define 2 lists for the keys and for the pointers to the other nodes.

To insert into a B-Tree.

Now let's look at adding into a B-Tree. There are 2 cases we need to look at first.

1. Insert into a non-leaf node.
1. If passed a key, we compare the key against the nodes stored keys and find which pointer we should pass this value on to.
2. If this is a key and a node, we need to add the key to our keys and the node to our nodes. Then check to see if our key list is too large.
1. If not too large, do nothing.
2. Else,
1. We split the keys into 2 lists (leftSide and rightSide) where the pivot is the median key. 
2. Create a new node with  the key list from the rightSide.
3. Check if we are the root node, if we are, create a new empty root node.
4. Pass the new node and the median key to our parent node.
2. Insert into a leaf node. Compare key against the stored keys, insert the key into the list. Check if the size of the stored keys is greater than 2d.
1. If No, Finish.
2. If Yes,
1. Split the keys into 2 lists (leftSide and rightSide) where the pivot is the median key. 
2. Create a new node with  the key list from the rightSide.
3. Check if we are the root node, if we are, create a new empty root node.
4. Pass the new node and the median key to our parent node.

That's pretty much it. It's a bit confusing as pseudo code, so let's look at the code for it

If we break this down.

Line 3: We find the position within where this key is compared to our keys.
Line 9: We check if there if this node is a leaf.
Line 11: If we aren't a leaf we insert the key into our list of keys.
Line 12: We check if the key list is now too large.
Line 14-29: We split the keys and create a new node.
Line 31: We check to see if we have a parent.
Line 36: Finally we insert the pivot key and the node into our parent.
Line 42: If we aren't a node we pass the key along.


So now we have to deal with insertion for non-leaf nodes.
Once again let's break this down.
Line 3: We find the position where this key is compared to our keys.
Line 8-9: We insert the key and the node into our lists at the correct spot.
Line 12: Check to see if we're over the maximum
Line 14-43: We split the keys and the pointers based on the median then create a new node.
Line 47: Passed the new key value and the new node to our parent to deal with.

This is how we insert into a B-Tree.

Get a value from a B-Tree.

This should be fairly self-explanatory.

Conclusion

OK, so now we have a very basic in-memory C# B-Tree, I've uploaded the source for it. It's not particularly useful yet, however it should be good enough for us to start building on. The next step will be to tidy up the code and leverage some of the observations about the structure to make improvements, when move to a B+-Tree structure and beyond.

The code can be found at GitHub